RMUC2022运动补偿
- Authors
Ligcox, Li
- Contact
- Date
2022/08/14
- Copyright
This document has been placed in the public domain.
概述
在RMU竞赛中,机器人自身的运动会对自瞄系统产生极大的偏差。该文档阐述了通过运动补偿模块,消除由于哨兵机器人自身底盘运动对自瞄系统产生的偏差。
流程
TODO
坐标系定义
云台坐标系通过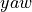 轴与
轴与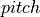 轴连接在底盘上,初始坐标系
轴连接在底盘上,初始坐标系 。
。
其中:前方为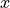 正方向,左方为
正方向,左方为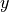 正方向,上侧为
正方向,上侧为 正方向。重力加速度
正方向。重力加速度 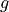 方向为
方向为  轴负方向。
轴负方向。
数学推导
在 中:
中:
 中空间目标点
中空间目标点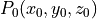 、
、![\vec{v}_0 = [v_{x_0}, v_{y_0}, v_{z_0}]^\top](../_images/math/260912329a89f065b7c720094bb1fa3a038add1b.png) 在变换矩阵
在变换矩阵 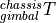 作用下,
变换为
作用下,
变换为 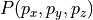 、
、![\vec{v} = [vx, vy, vz]^\top](../_images/math/8bc095d999b4bd806110594956bcc05e0f678477.png) ,空间向量
,空间向量![\overrightarrow{O_{gimbal}P}=[p_x, p_y, p_z]^\top](../_images/math/13063c63779bb4ee3018e3c739307e971e68ef8a.png) 。
其中:
。
其中:
![^{chassis}_{gimbal}T = \left[\begin{array}{ccc} ^{chassis}_{gimbal}R & ^{chassis}_{gimbal}p \\ 0 & 1 \end{array}\right]](../_images/math/a54b838132ba3464727b719fe95654c93a4c6138.png)
弹丸初速度 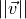 通过裁判系统获得,一般地:
通过裁判系统获得,一般地: 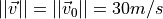
弹丸在空中飞行时间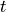
底盘速度 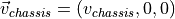
经过修正后,云台偏转角度在底盘坐标系下的偏转角度为 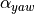 和
和 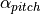 。
。
根据几何关系,有:
![\overrightarrow{O_{gimbal}P} = \left[\begin{array}{ccc}
p_x \\ p_y \\ p_z
\end{array}\right] =
\left[\begin{array}{ccc}
||\vec{v}||t\cos \alpha_{pitch} \cos \alpha_{yaw} \\
||\vec{v}||t\cos \alpha_{pitch}\sin \alpha_{yaw} + v_{chassis}t \\
-||\vec{v}||t\sin \alpha_{pitch} - \frac{1}{2} gt^2 \\
\end{array}\right]
\Longrightarrow \\
\frac{1}{4}g^2 t^4+(v_{chassis}^2-gp_z-||\vec{v}||^2)t^2 - 2p_y v_{chassis}t + ||\overrightarrow{O_{gimbal}P}||^2 = 0](../_images/math/0da863223df970d178d7d3e16a77001b35323052.png)
则:
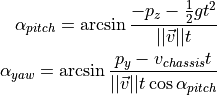
由于云台 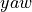 轴与
轴与 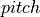 轴刚性连接到底盘,云台在底盘坐标系下偏转角度
轴刚性连接到底盘,云台在底盘坐标系下偏转角度 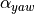 和
和 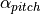 即为云台相对于当前位置偏转角度。
即为云台相对于当前位置偏转角度。
功能实现
Note
运动补偿的相关代码位于 bubble_contrib/bubble_aming 模块下
变换矩阵 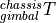 通过机器人URDF文件及当前偏转绝对角度通过tf tree获取。
通过机器人URDF文件及当前偏转绝对角度通过tf tree获取。
目标点 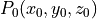 信息通过识别器经由 PnP解算 获得。
PnP解算将世界坐标系下目标的位姿信息转换为相机坐标系下:
信息通过识别器经由 PnP解算 获得。
PnP解算将世界坐标系下目标的位姿信息转换为相机坐标系下:
![\left[\begin{array}{c}X_{c} \\ Y_{c} \\ Z_{c} \\ 1\end{array}\right]=\left[\begin{array}{cccc}r_{11} & r_{12} & r_{13} & t_{x} \\ r_{21} & r_{22} & r_{23} & t_{y} \\ r_{31} & r_{32} & r_{33} & t_{z} \\ 0 & 0 & 0 & 1\end{array}\right]\left[\begin{array}{c}X_{w} \\ Y_{w} \\ Z_{w} \\ 1\end{array}\right]](../_images/math/2c603f7ef320253d11f23d8aad618380a1818b6b.png)
对于实际使用的目标在  下的位姿估计值,由于相机坐标系与云台坐标系存在平移偏移。
实现过程中,解算结果的
下的位姿估计值,由于相机坐标系与云台坐标系存在平移偏移。
实现过程中,解算结果的 tvec 为目标在云台坐标系(更准确地说是在弹丸射出的摩擦轮位置坐标系)的位姿信息。
此外,在进行补偿的过程中, 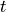 为弹丸射出后击中目标的时间,而
为弹丸射出后击中目标的时间,而  原点位于机器人底盘的几何中心。
因此,实际求解过程中使用的
原点位于机器人底盘的几何中心。
因此,实际求解过程中使用的 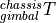 与数学推导中有一定的变化。
与数学推导中有一定的变化。
tf tree获取的 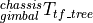 为:
为:
![^{chassis}_{gimbal}T_{tf\_tree} = \left[\begin{array}{ccc} ^{chassis}_{gimbal}R & ^{chassis}_{gimbal}p \\ 0 & 1 \end{array}\right]](../_images/math/54554e5f8b4bb8d3c47c7a48c5e4d717614a35cc.png)
实际使用的 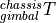 为:
为:
![^{chassis}_{gimbal}T_{tf\_tree} = \left[\begin{array}{ccc} ^{chassis}_{gimbal}R^\top & 0 \\ 0 & 1 \end{array}\right]](../_images/math/1b044c7124cda6a0752c82705b63baf500cb75eb.png)
获得 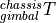 后,
能够求解空间向量
后,
能够求解空间向量![\overrightarrow{O_{gimbal}P}=[p_x, p_y, p_z]^\top](../_images/math/13063c63779bb4ee3018e3c739307e971e68ef8a.png) 。
。
通过numpy的 numpy.poly1d 模块,
求解含 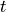 多项式
多项式 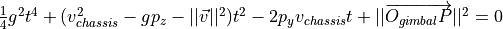 的解。
的解。
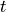 应当包含4个解,刨除两个负数解后,
应当包含4个解,刨除两个负数解后, 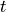 的剩余解分别弹丸在瞄准姿态和抛射姿态击中目标的时间。取其中较小的一个,即为所求时间
的剩余解分别弹丸在瞄准姿态和抛射姿态击中目标的时间。取其中较小的一个,即为所求时间 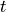 。
。
一般的, 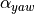 和
和 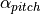 值域均为
值域均为 ![[-\frac{\pi}{2}, \frac{\pi}{2}]](../_images/math/06a3c9ec2e9a4182e301bc653c243e576632be68.png) ,因此使用
,因此使用 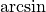 求解。
求解。
结语
文档阐述了当前版本Bubble中运动补偿模块实现的过程,通过对向量  的修改,还能够消除云台运动、空气阻力等对弹丸飞行造成的影响。
的修改,还能够消除云台运动、空气阻力等对弹丸飞行造成的影响。